Cryptography解题报告:Factor the RSA modulus
这次的题目花了好多时间去读题啊,居然是所!有!作业中!最长的题目!!光是阅读题目理解题意都花了一半以上时间。题目要求对两个很接近的素数合成的N进行分解,借此告诫我们不能自己设计不可靠的crypto方案。
Question_1
首先让大家看看原题目感受感受英语的气息
We show that the resulting RSA modulus N=pq can be easily factored.
Suppose you are given a composite N and are told that N is a product of two relatively close primes p and q, namely p and q satisfy
$$|p-q|<2N^{1/4}\quad (*)$$
Your goal is to factor N.
Let A be the arithmetic average of the two primes, that is
$$A=\frac{p+q}{2}$$
Since p and q are odd, we know that $p+q$ is even and therefore $A$ is an integer.
To factor N you first observe that under condition (*) the quantity $\sqrt{N}$ is very close to $A$. In particular, we show below that:
$$A-\sqrt{N}<1$$For completeness, let us see why $A-\sqrt{N}<1$. This follows from the following simple calculation.
First observe that$A^2-N=(\frac{p+q}{2})^2-N=(\frac{p-q}{2})^2=(p-q)^2/4$
Now, we obtain $A-\sqrt{N}=\frac{A^2-N}{A+\sqrt{N}}=\frac{(p-q)^2/4}{A+\sqrt{N}}$
Since $\sqrt{N}\le A$ it follows that $A-\sqrt{N}\le\frac{(p-q)^2/4}{2\sqrt{N}}$
By assumption (*) we know that $(p-q)^2<4\sqrt{N}$ and therefore $A-\sqrt{N}\le \frac{4\sqrt{N}}{8\sqrt{N}}=\frac{1}{2}$since $A$ is an integer, rounding $\sqrt{N}$ up to the closest integer reveals the value of $A$. In code, $A=ceil(sqrt(N))$ where "ceil" is the ceiling function.
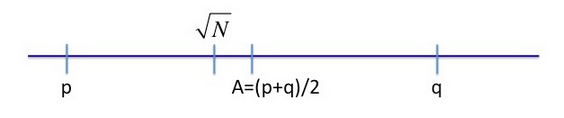
Visually, the numbers $p,q,\sqrt{N}$ and $A$ are ordered as follows:
There is an integer x such that $p=A−x$ and $q=A+x$.
But then $N=pq=(A-x)(A+x)=A^2-x^2$ and therefore $x=\sqrt{A^2-N}$
Now, given $x$ and $A$ you can find the factors p and q of N since $p=A−x$ and $q=A+x$. You have now factored N !
In the following challenges, you will factor the given moduli using the method outlined above. To solve this assignment it is best to use an environment that supports multi-precision arithmetic and square roots. In Python you could use the gmpy2 module. In C you can use GMP.
读完没有?是不是题目有点长!!我用自己的CET6翻译水平大致翻译一下:
通常情况下,组成RSA的两个素数p、q是独立生成的,假设一个程序员使用随机算子R生成了一个素数p,他紧接着用R+1作为算子生成q,导致p和q非常接近。今天的任务是利用“生成pq非常接近”这个漏洞进行分解质因数N=pq。假设pq满足$|p-q|<2N^{1/4}$ 这个条件。
令$A=\frac{p+q}{2}$ ,因为p、q都是偶数,所以A是整数。
为了分解质因数,首先观察(*)条件,我们可以推理得出$A-\sqrt{N}< 1$,推导如下:(这里就不翻译了,用到了两个公式:平方差公式、算术-几何平均数公式)
因为A是整数,对$\sqrt{N}$ 进行向上四舍五入即可得出A的值。如数轴所示:(上面的图)
假设有一个整数x,满足 $p=A−x$ 和 $q=A+x$,因此推理得 $x=\sqrt{A^2-N}$
现在你手上有了x和A,就可以分解质因数N了,非常快速。
这里程序要用到高精度运算库,python可以使用gmpy2,C\C++可以使用GMP,Java可以使用BigInteger。
现在给你N,和条件$|p-q|<2N^{1/4}$ (*),请写出分解得到p、q中较小的那个数。
N = "179769313486231590772930519078902473361797697894230657273430081157732675805505620686985379449212982959585501387537164015710139858647833778606925583497541085196591615128057575940752635007475935288710823649949940771895617054361149474865046711015101563940680527540071584560878577663743040086340742855278549092581"
解题思路:只需要按部就班把教授说的计算一次即可。
$a=\sqrt{N};$
$A=ceil(a);$
$x=\sqrt{A^2-N};$
$p=A-x,q=A+x;$
$output\quad smaller(p,q);$
Question_2
题目:同样求出分解出p、q,不过这个条件(*)改为
$$|p-q|<2^{11}N^{1/4}$$
推理过程
与Question #1一致,我们令 $A=\frac{p+q}{2}$ ,得出 $A^2-N=(p-q)^2/4$ 。
代入 $A-\sqrt{N}=\frac{(p-q)^2/4}{A+\sqrt{N}}\le \frac{(p-q)^2/4}{2\sqrt{N}}$
得到 $A-\sqrt{N}\le (p-q)^2/8\sqrt{N}$
由于条件(*)等价于 $|p-q|^2< 2^{11}\sqrt{N}$,代入上式
得到 $A-\sqrt{N}<2^{19}$
我们需要将A穷举$2^{19}$次就可以得出结果了
$i=ceil(\sqrt{N});$
$for\quad a\quad in\quad i\quad to\quad i+2^{19}: $
$\quad x=\sqrt{a^2-N};$
$\quad p=(a+x);q=(a-x);$
$\quad test\quad if\quad N=pq\quad break;$
$output\quad p,q;$
Question_3
题目:分解N,条件(*)改为
$$|3p-2q|< N^{1/4}$$
这题目变得是更一般的推理过程了。比较灵活。
推理过程
令 $A=3p+2q$(为什么?是因为使得A为整数)得出 $A^2-24N=(3p-2q)^2$
代入 $A-\sqrt{24N}=\frac{(3p-2q)^2}{A+\sqrt{24N}}\le \frac{(3p-2q)^2}{2\sqrt{24N}}$
得到 $A-\sqrt{24N}\le \frac{1}{2}$
因此得到 $A=ceil(\sqrt{24N})$,然后根据$A=3p+2q$逆着推出p和q
假设存在x,使得 $p=\frac{A+x}{6}$ 和 $q=\frac{A-x}{4}$
那么 $N=pq=\frac{(A+x)(A-x)}{24}$
所以 $x^2=A^2-24N$ ,即 $x=\sqrt{A^2-24N}$
那么既然知道了A和x,就可以算出p和q
类似Question1,我们写出下面的伪代码
$a=\sqrt{24N};$
$A=ceil(a);$
$x=\sqrt{A^2-24N};$
$p=\frac{A-x}{6},q=\frac{A+x}{4};$
$output\quad smaller(p,q);$
Question_4
又来感受一下题目:
The challenge ciphertext provided below is the result of encrypting a short secret ASCII plaintext using the RSA modulus given in the first factorization challenge.
The encryption exponent used is $e=65537$. The ASCII plaintext was encoded using PKCS v1.5 before the RSA function was applied, as described in PKCS.
Use the factorization you obtained for this RSA modulus to decrypt this challenge ciphertext and enter the resulting English plaintext in the box below. Recall that the factorization of N enables you to compute $\phi(N)$ from which you can obtain the RSA decryption exponent.Challenge ciphertext (as a decimal integer):
220964518674103817763065611348834180174100697878928232......After you use the decryption exponent to decrypt the challenge ciphertext you will obtain a PKCS1 encoded plaintext. To undo the encoding it is best to write the decrypted value in hex. You will observe that the number starts with a '0x02' followed by many random non-zero digits. Look for the '0x00' separator and the digits following this separator are the ASCII letters of the plaintext.
让我给大家翻译一下:
这次的挑战是给你一个RSA加密的密文,其明文为ASCII字符,加密因子$e=65537$,它的RSA modulus是Question1中的N,明文使用PKCSv1.5进行padding,然后才进行RSA函数加密,详见RCF2313文档定义的加密方式。
请你使用分解质因数的方法来把明文解出来。回想一下分解得到p和q以后怎么样得到$\phi(N)$ ,然后计算出解密因子$d$。
调用RSA函数正确解密后,你将获得一个PKCSv1.5编码的明文,要想正确解密,最好将其转成hex编码,你会发现它是以0x02开头的数据,其后跟着一大堆非0x00的十六进制数,寻找0x00作为padding分隔符,剩下的内容就是ASCII明文。
推理过程
由于题目给出了N=pq,而且p和q在Question1中已经求出来了,剩下的内容非常简单
根据 $\phi(N)=(p-1)(q-1)$ 就能解出$\phi(N)$
由 $ed=1\pmod{\phi(N)}$ 求出解密因子$d$
由 $(msg^e)^d = msg \pmod{N}$ 可以知道,将密文做幂运算就能得到明文
将明文转成十六进制,从0x00开始截取字符串到末尾,就能出结果了
伪代码:
$fi=(p-1)(q-1);$
$d=invert(e)\pmod{fi};$
$PlainText=(CipherText)^d\pmod{N};$
$PlainText_h=dec2hex(PlainText);$
$index=PlainText_h.find(0\times00);$
$output\quad PlainText_h[index:;];$
关于怎么样把一个大整数转成hex编码,可以参考进制转换的写法,利用GMP大数库进行转换,一句话就ok
mpz_get_str(PlainText,16,mpz_t_PT); //转成16为底的字符串
程序源码
因为我之前用过GMP,因此今次还是使用C++编写。效率也很高。这里给出我的程序。
Question_1.cpp
Question_2.cpp
Question_3.cpp
Question_4.cpp
运行结果:
Question_1
13407807929942597099574024998205846127479365820592393377723561443721764030073662768891111614362326998675040546094339320838419523375986027530441562135724301
Question_2
25464796146996183438008816563973942229341454268524157846328581927885777969985222835143851073249573454107384461557193173304497244814071505790566593206419759
Question_3
21909849592475533092273988531583955898982176093344929030099423584127212078126150044721102570957812665127475051465088833555993294644190955293613411658629209
Question_4
Factoring lets us break RSA.
结束语
Week6就要结束了,这门课就完成了,接下来还有Cryptography II,很是期待。
2015年年末,为了看懂shadowsocks源码里面的crypto实现部分,我决定去Coursera学习密码学。就出于这种好奇心,完成这门课程我花费了三个多月,到2016年4月才完成,我是注册两个班,第一次班是没时间去上视频公开课,于是把视频下载回来,有空就看,第二个班我就认真开始上课仔细做笔记学习,确实学得很多东西,加密这东西,与每个人的信息安全息息相关。
今天我已经能很自豪地说,我已经能看懂shadowsocks里面很多代码了(我的ss项目),也懂得ss作者设计这个软件的初衷——让每个人有自由去追求他想要的东西,无论是知识还是财富亦或是facebook上点赞的虚荣心。
不管怎么样,多学习是有益的,即使不能马上用到新知识,始终有一天会派上用场的!
附:Dan Boneh教授经典语录,回味无穷,哈哈哈!
You should never ever try to invent your own cryptographic system unless you have mastered the science of Mathematics, Cryptography, and Computers.
I will show you a "cute attack".
If any of you can come up with an algorithm to factor composites to prime factors, again, as I said, it's an instant fame in the crypto world. And it would have tremendous impact on Security of the Web general.